2.4.6 二次方的算法性能

现在考虑一个类似的问题：两个n位的整数相乘。例2-4展示了使用小学课堂上学过的算法实现的乘法运算，其中n位数字的表示方法与之前的加法一样。

例2-4：mult乘法的Java实现 public static void mult (int[] n1, int[] n2, int[] result) { int pos = result.length-1; // 清除所有的值 for (int i = 0; i < result.length; i++) { result[i] = 0; } for (int m = n1.length-1; m>=0; m--) { int off = n1.length-1 - m; for (int n = n2.length-1; n>=0; n--,off++) {

int prod = n1[m]*n2[n];   // 计算部分和，并且加上进位  result[pos-off] += prod % 10;  result[pos-off-1] += result[pos-off]/10 + prod/10;  result[pos-off] %= 10;}

}

} 同样的，这里也会给出另外一种实现算法——times。这种算法避免了取模运算的高费用，并且忽略了当n1[m]等于0时不必要的内层计算（注意，这里并没有给出times算法实现，读者可以在提供的代码库中找到它）。times算法包含了203行生成的Java代码来消除两个取模操作。那么在需要额外的费用维护和管理生成代码时，这种衍生算法还能够减少总的性能费用吗？表2-4给出了这些乘法算法的性能，乘法所使用的数据与加法使用的随机生成数据一致。图2-4采用图形化的方式来描述算法性能，可以看到，抛物曲线是平方级算法的典型标志。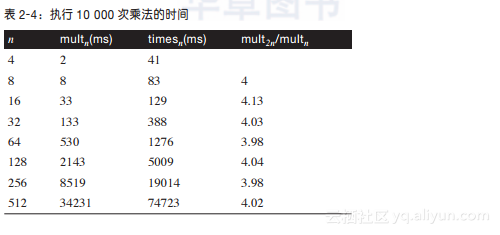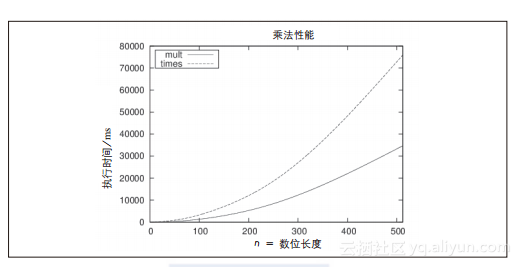图2-4：比较mult和times如图2-4所示，虽然times衍生算法的速度是mult算法的1/2，但是times和mult展现了相同的渐近性能。mult2n / multn的比率大约是4，这证明了乘法的性能是平方级的。我们定义t(n)表示乘法算法在输入规模为n时的实际执行时间。根据这个定义，对于所有的n > n0来说，必然存在某些常数c（c > 0），满足t(n) ≤ c*n2。我们不需要知道c和n0的实际值是多少，只需要知道它们必然存在即可。这个mult算法实现在我们的平台上执行时，常数c为1/7，n0为16。需要再次说明的是，修改算法实现来提升效率并不会改变算法是平方级性能的事实。尽管如此，还是有其他的算法（Zuras，1994）可以让n位数相乘的明显速度快于平方级。对于像数据加密这种需要频繁实现大数乘法的应用，这类算法非常重要。